Each box is equipped with a matrix of 16 A/C light bulbs that are used as a display. Inside each box there is a micro controller that is able to control each light bulb discretely and communicate with the other box over serial connection. The two microcontrollers are playing a game with each other.

Battle guesses the future state of the other machine. This is attempted by using something like a Markov chain. Both of the machines share a common lexicon of 13 possible patterns. The game consists of the machines taking turns creating and displaying sequences of patterns. Each sequence is 10 patterns long. A turn is composed in three steps.

1. Read the incoming sequence, what are the transition probabilities ( what is the distribution of transitions from one pattern to the next divided by the number of patterns in the sequence )?
2. Given the transition probabilities and a random starting state taken from the input sequence, construct a new sequence 10 patterns long that is most probable continuation of the input sequence.
3. Send the new pattern to the other machine and wait for more input.

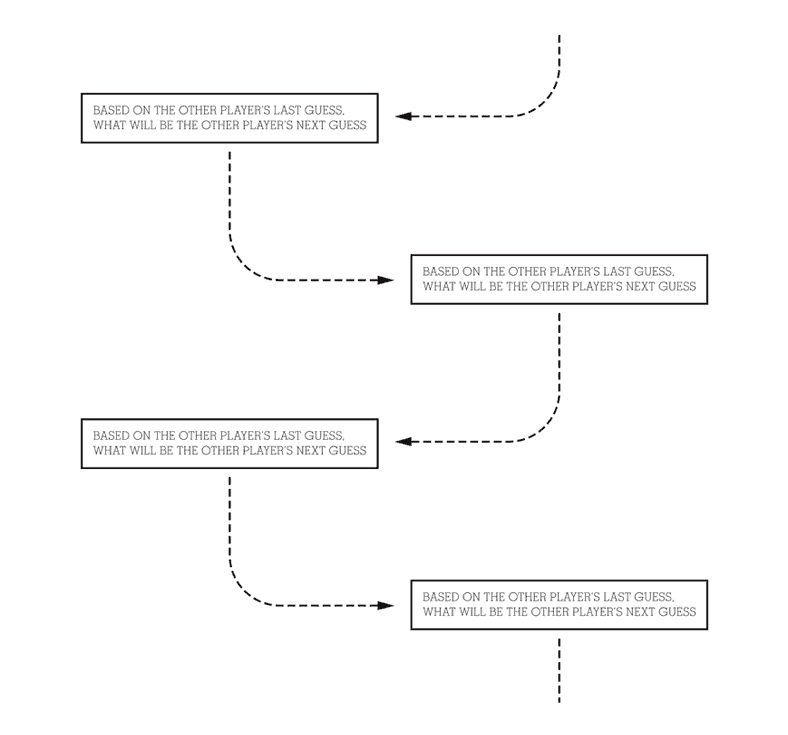
When one of the boxes constructs a sequence that is identical to the input sequence, that box has lost the game. At that point it will flash its columns from left to right and then construct a completely random sequence to start the game over. The box that won never knows that it won, it continues with the game as if it never ended.

Here’s a video of the two machines in action:

I used the Sanguino microcontroller board for this project because it was cheap, it has lots of i/o pins, and it has two hardware serial ports. I used cat 6 cable and fixtures to connect the serial ports of the two machines together and to upload code from my computer.

I had never built a project that uses two microcontrollers talking to each other so I had to look around for something similar to get an idea of the best way to do it. I found MeggyChip a game written by Chris Brookfield and Windell Oskay for the excellent Meggy Jr game platform. I was able to use the communication protocol from that game with a little modification.

Here’s my awkward attempt at implementing some kind of Markov like process. It mostly works but I had to fudge it a little because for some reason there was a tendency for the machines to converge on the first pattern in the lexicon:

[cc lang=”c”]
void markov()
{
countInComingSequence();
buildNewSequence();
}

void countInComingSequence()
{
//we need to know how many times each pattern appears so we can divide transitions by it later
//first clear out wordOccurenceSum
for(byte i=0; i < NumPatterns; i++) wordOccurenceSum[i] = 0;

//then add up the number of times each pattern appears
for(byte i=0; i < TurnLength; i++) wordOccurenceSum[inboundBytes[i]]++;

//this is to clear out transitionTotals array
for(byte i=0; i < NumPatterns; i++)
{
for(byte j=0; j < NumPatterns; j++)
{
transitionTotals[i][j] = 0;
}
}

//this keeps track of how many times each transition occurs
for(byte i=0; i < TurnLength; i++)
{
transitionTotals[inboundBytes[i]][inboundBytes[i+1]]++;
}

//lets empty out the transitionProbability array so we can make new stats
for(byte i=0;i<NumPatterns;i++)
{
for(byte j = 0; j<NumPatterns;j++)
{
transitionProbability[i][j] = 0.00;
}
}

//now we need to take the number of times a transition happended and divide it by
//the number of times an inital state appears in the sequence to get the probability
//of that transition happening
for(byte i=0; i < NumPatterns; i++)
{
//this is special case for the beginning the iteration
float tempA = wordOccurenceSum[i];
float tempB = transitionTotals[i][0];
transitionProbability[i][0] = tempB/tempA;

for(byte j=1; j < NumPatterns; j++)
{
tempA = wordOccurenceSum[i];
tempB = transitionTotals[i][j];

//add up the percentage for every step in the iteration
transitionProbability[i][j] = transitionProbability[i][j – 1] + tempB/tempA;
}
}
}

void buildNewSequence()
{

//this is to start out with a random outbound:
for(byte i = 0;i< TurnLength; i++) outboundBytes[i] = random(0,14);

//start the sequence with the last position of incomming bytes
outboundBytes[0] = inboundBytes[random(0,13)];

//for the second position and on look at the last position and randomly choose from the most probable transitions
for(byte i=1; i< TurnLength; i++)
{
randomSeed(analogRead(0));
float rnd = random(2,11);
rnd = rnd/10;
for (byte j = 0; j < NumPatterns; j++)
{
if (rnd <= transitionProbability[outboundBytes[i-1]][j])
{
//throw a monkey wrench in the zero bias 🙁
if(j==0) j = random(0,5);
outboundBytes[i] = j;
break;
}
}
}
boolean different = false;
for(byte i=0; i< TurnLength; i++)
{
if(outboundBytes[i]!=inboundBytes[i]) different = true;
}
if (different == false)
{
//this means that I loose so restart the game
splashScreen();
splashScreen();
delay(500);

//start over by making a new random sequence for us to guess
for(byte i = 0;i< TurnLength; i++) outboundBytes[i] = random(1,14);
}
}
[/cc]

You can download the code for the whole project here:
http://github.com/taboularasa/battle/